КК VS блокчейн. Часть II. Квантовые атаки на Биткоин и способы защиты от них

Дисклеймеры по переводу

Ссылка на оригинал прямая: https://arxiv.org/pdf/1710.10377v1.pdf.  Первое: поскольку начальный документ написан в pdf-формате, а Hub.Forklog требует стандартной html/markdown-разметки, ряд моментов пришлось упустить, включая ссылки/сноски, а равно отображение спецсимволов.  Второе важное замечание заключается во времени, а точнее — периоде обработки: у меня фактически вырисовывалась картина по этому исследованию, исходя из разных работ, ссылающихся на него, поэтому ряд моментов сократил (но незначительно), чтобы убрать очевидные вещи, а ряд — заменил на более понятные Web 3.0 термины. Но в остальном (в 95% случаев) оставил перевод почти дословным, меняя слова лишь при важности передачи смысловой/логической нагрузки, поскольку времени на длительную обработку текста попросту нет, а значимость его переоценить сложно, — понятие брал по wiki-определениям с отсылками.  Третье — почти все расчёты убрал, поскольку переводить формулы — довольно странное занятие :), поэтому, если они для вас важны в написании именно и форме передачи, обратитесь к оригиналу.

Преамбула

Ключевые криптографические протоколы, используемые сегодня для защиты в Интернете, включая и финансовые транзакции, могут быть атакованы при создании достаточно универсального квантового компьютера (КК). Одной из конкретных областей (подобного) риска являются криптовалюты… Мы исследуем риск атак КК на биткоин [напомню: с заглавной буквы — сеть (Биткоин), с прописной — монета (биткоин с тикером BTC)] и другие криптовалюты. Мы обнаружили, что доказательство работы (PoW), используемое в Bitcoin, относительно устойчиво к … (атакам через) квантовые компьютеры (КК) в ближайшие 10 лет, в основном потому, что специализированные ASIC-майнеры чрезвычайно быстры по сравнению с предполагаемой тактовой частотой КК ближайшего будущего. С другой стороны, схема подписи на эллиптических кривых, используемая в Bitcoin, подвержена гораздо большему риску и может быть полностью разрушена КК уже в 2027 году, по самым оптимистичным оценкам. Мы анализируем альтернативное доказательство работы под названием Momentum, основанное на поиске коллизий в хэш-функции, которое ещё более устойчиво к атакам посредством КК. Мы также анализируем доступные схемы подписи через постквантовые технологии, чтобы понять, какая из них лучше всего отвечает требованиям безопасности и эффективности приложений блокчейна.

I. ВВЕДЕНИЕ

Биткоин — децентрализованная цифровая валюта, защищённая криптографией. С момента разработки Сатоши Накамото в 2008 году, Биткоин оказался удивительно успешной и безопасной системой и вдохновил разработку сотен других криптовалют и блокчейн-технологий на рынке… Безопасность Биткоина обусловлена несколькими особенностями его протокола.  Во-первых, это доказательство выполнения работы (PoW), которое требуется для записи транзакций леджер Биткоина. Необходимая для этого работа защищает злоумышленников, обладающих менее чем 50% вычислительной мощности сети, от создания альтернативной истории транзакций. Во-вторых, это криптографическая подпись, которая используется для авторизации транзакций. В настоящее время в Bitcoin используется схема подписи, основанная на эллиптических кривых. Грядущее развитие КК представляет серьёзную угрозу почти для всех криптографических средств, используемых в настоящее время для защиты Интернета и финансовых транзакций, а также для Bitcoin. В этой статье всесторонне анализируем уязвимость Bitcoin к квантовым атакам. Мы обнаружили, что используемое в Биткоине доказательство работы относительно устойчиво к (атакам) КК в ближайшие 10 лет, главным образом потому, что специализированные ASIC-майнеры чрезвычайно быстры по сравнению с предполагаемой тактовой частотой квантовых компьютеров ближайшего будущего. Это означает, что транзакции, попавшие в блокчейн, будут относительно защищены даже в присутствии КК. Известно, что схема подписи на эллиптической кривой, используемая в Bitcoin, может быть нарушена (атакована) алгоритмом Шора для вычисления дискретных логарифмов. Мы проанализировали, сколько времени может потребоваться для получения секретного ключа из опубликованного открытого ключа на будущем КК. Это очень важно в контексте Биткоина, так как основное окно для этой атаки — время с момента трансляции транзакции до её обработки в блок в блокчейне и нескольких блоков после неё. По нашим самым оптимистичным оценкам, уже в 2027 году может появиться КК, способный взломать схему подписи эллиптической кривой менее чем за 10 минут — время «сбора» блока, используемого в Биткоине. Мы также предлагаем некоторые контрмеры, которые можно предпринять для защиты Bitcoin от квантовых атак. Мы анализируем альтернативную схему доказательства выполнения работы под названием Momentum, основанную на поиске коллизий в хэш-функции, и показываем, что она допускает даже меньше атак посредством КК, чем доказательство выполнения работы, используемое в Bitcoin. Мы также рассматриваем альтернативные схемы подписи, которые считаются квантово безопасными. 

II. ОСНОВЫ БЛОКЧЕЙНА

В этом разделе мы даём базовый обзор работы Биткоина, чтобы мы могли ссылаться на конкретные части протокола при описании возможных квантовых атак. Мы будем вести обсуждение на абстрактном уровне, поскольку многие принципы применимы и к другим криптовалютам с такой же базовой структурой, как у Биткоина. Все транзакции Bitcoin хранятся в публичной бухгалтерской книге (леджере / блокчейне), называемой блокчейн. Отдельные транзакции объединяются в блоки, и считается, что все транзакции в блоке произошли в одно и то же время [Menaskop: хотя как раз важно, что это НЕ так]. Эти транзакции упорядочиваются по времени, помещаясь в цепочку. Каждый блок в цепочке (кроме самого первого, или генезис-блока) имеет указатель на предыдущий блок в виде хэша заголовка предыдущего блока. Блоки добавляются в цепочку майнерами. Майнеры могут объединять необработанные транзакции в блок и добавлять их в цепочку, выполняя доказательство работы (PoW). Биткоин и многие другие монеты используют PoW, разработанный Адамом Бэком (в проекте) под названием Hashcash. PoW в Hashcash заключается в поиске правильно сформированного заголовка блока, такого, что h(header) ≤ t, где h — криптографически безопасная хэш-функция, а header — заголовок блока. Верно сформированный заголовок содержит краткую информацию о блоке, такую как хэш, полученный из транзакций в блоке 1, хэш заголовка предыдущего блока, метку времени, а также так называемый nonce — 32-битный регистр, который может быть выбран произвольно. Иллюстрация блока приведена в таблице I. Параметр t — целевое значение, которое может быть изменено для регулировки сложности PoW. В Биткоине этот параметр динамически изменяется каждые 2016 блоков таким образом, что в среднем сети требуется около 10 минут для решения PoW. ТАБЛИЦА I. Иллюстрация блока. Данные в верхней части представляют собой заголовок блока. В Биткоине хэш-функция, выбранная для доказательства работы, представляет собой два последовательных применения хэш-функции SHA256: {0, 1}∗ → {0, 1}256, то есть h(-) = SHA256(SHA256(-)). Поскольку размер диапазона h равен 2256, ожидаемое количество хэшей, которое необходимо попробовать для выполнения хэш-доказательства работы с параметром t, равно 2256/t. Вместо параметра t, доказательство работы Биткоина обычно задается через термин сложности D, где D = 2224/t. Это ожидаемое количество хэшей, необходимое для завершения доказательства работы, делённое на 232, количество доступных несов. Другими словами, сложность — ожидаемое количество вариаций транзакций и временных меток, которые необходимо попробовать при хэшировании заголовков блоков, когда для каждой фиксации транзакций и временной метки будут опробованы все nonce-ы. Майнеры могут объединять необработанные транзакции в блок, как им заблагорассудится, и получают определённое количество биткоинов за успешное выполнение задачи PoW. Транзакция «генерации» (добычи), выплачивающая вознаграждение за майнинг, также является транзакцией, включенной в блок, что гарантирует, что разные майнеры будут искать в разных заголовках блока верный предварительный хэш-образ. Как только майнер находит заголовок, соответствующий h(header) ≤ t, он сообщает об этом в сеть, и блок добавляется в цепочку. Обратите внимание, что проверить, что заявленный заголовок удовлетворяет условию PoW, очень просто — для этого достаточно выполнить одну оценку хэш-функции. Цель PoW заключается в том, чтобы одна сторона не могла в одностороннем порядке манипулировать блокчейном с целью, например, двойного расходования средств. В блокчейне возможны форки, но в любой момент времени протокол предписывает майнерам работать над тем форком, который в данный момент является самым длинным. Как только блок имеет k-блоков, следующих за ним в самой длинной [Menaskop: правильней в цепи с наибольшей проделанной работой] цепи, сторона, которая хочет создать самую длинную цепь, не включающую этот блок, должна будет выиграть гонку PoW, начиная с k блоков позади. Если сторона контролирует меньше половины вычислительной мощности сети, то с ростом k это становится маловероятным. В Биткоине транзакция обычно считается безопасной, когда за ней следуют 6 блоков [Menaskop: проще говоря, подтверждение — через 6 блоков считается условно-безопасным]. Первый вопрос… заключается в том, какое преимущество будет иметь КК при выполнении подобной работы, и сможет ли он в одностороннем порядке «зайти со спины» и манипулировать блокчейном. Второй важный для нас аспект Биткоина — форма, которую принимают транзакции. Когда Боб хочет отправить биткоин Алисе, Алиса сначала создаёт (в идеале — новую) пару закрытый-публичный ключ. Открытый ключ хэшируется для создания адреса. Этот адрес Алиса предоставляет Бобу в качестве адреса для отправки биткоина. Биткоин использует хэш открытого ключа в качестве адреса вместо открытого ключа не из соображений безопасности, а просто для экономии места. Как мы увидим позже, этот выбор дизайна архитектуры действительно влияет на квантовую безопасность. Чтобы отправить биткоин Алисе, Боб должен также указать транзакции в блокчейне, где биткоин был отправлен на адреса, которые он контролирует. Сумма биткоинов, полученных по этим указанным транзакциям, должна составлять не менее суммы биткоинов, которую Боб хочет отправить Алисе. Боб доказывает, что владеет этими адресами, указывая открытый ключ, соответствующий каждому адресу, и используя свой закрытый ключ, соответствующий этому адресу, для подписания сообщения о том, что он передает эти биткоины Алисе.

III. Квантовые атаки на БИТКОИН 

A. Атаки на доказательство работы Биткоина

В этом разделе исследуем преимущество КК при выполнении PoW, используемого в Bitcoin. Наши выводы можно обобщить следующим образом: используя перебор методом Гровера, КК может выполнить PoW, выполнив вчетверо меньше операций, чем требуется классическому компьютеру. Однако, чрезвычайная скорость нынешнего специализированного оборудования ASIC для выполнения той же работы, в сочетании с гораздо более медленными прогнозируемыми скоростями для нынешних КК по существу сводит на нет это квадратичное ускорение на текущем уровне сложности, не давая КК никакого преимущества. Будущие усовершенствования квантовой технологии, позволяющие увеличить скорость до 100 ГГц, могут позволить КК решать те же задачи в 100 раз быстрее, чем нынешние технологии. Однако такое развитие событий маловероятно в ближайшее десятилетие, когда классические жёсткие диски станут намного быстрее, а квантовые технологии будут настолько широко распространены, что ни один агент с квантовой поддержкой не сможет доминировать в решении PoW-задач. Теперь подробно рассмотрим эти результаты. Напомним, что задача PoW в Биткоине состоит в том, чтобы найти правильный заголовок блока, такой, что h(header) ≤ t, где h(-) = SHA256(SHA256(-)). Безопасность блокчейна зависит от того, что ни один агент не сможет решить задачу PoW первым с вероятностью более 50%. Мы исследуем количество классических вычислительных мощностей, которые потребуются, чтобы сравняться с одним КК в выполнении этой задачи. Будем работать в модели случайного оракула, в частности, предположим, что Pr[h(header) ≤ t] = t/2256, где вероятность берётся равномерно по всем правильно сформированным заголовкам блоков, которые могут быть созданы с помощью транзакций, доступных в пуле в любой момент времени (такие сформированные заголовки блоков могут быть найдены путём варьирования nonce, транзакций, включённых в блок, а также младших битов временной метки заголовка). На классическом компьютере ожидаемое количество заголовков блоков и nonce, которые нужно хэшировать, чтобы найти нужный (результат), хэш-значение которого не превышает t, равно D × 232, где D — сложность хэширования, определяемая D = 2224/t. Для КК в модели случайного оракула можем ограничиться общим квантовым подходом к решению задачи PoW с помощью алгоритма Гровера. По алгоритму Гровера, поиск помеченного элемента в базе данных из N элементов может быть выполнен с помощью O(√N) множества запросов к базе данных (тогда как любой классический компьютер потребует Ω(N) запросов для выполнения той же задачи). Пусть N = 2256 — размер диапазона h для следующего. По нашим предположениям, с вероятностью не менее 0.9999 случайный набор из 10 — N/t множества заголовков блоков будет содержать по крайней мере один элемент, хэш которого не более t. Мы можем определить некоторую детерминированную функцию g, отображающую S = {0,1}⌈log(10-N/t)⌉ на отдельные хорошо сформированные заголовки блоков. Мы также определяем функцию f, которая определяет, является ли заголовок блока «хорошим» или нет E0 if h(g(x))>t f(x)= 1 if h(g(x))≤t . КК может вычислить f на суперпозиции входов, т.е. выполнить отображение Eαx|x⟩ → E(−1)f(x)αx|x⟩. Каждое применение этой операции называется вызовом оракула. Используя алгоритм Гровера, квантовый алгоритм может перебрать S, чтобы найти правильный заголовок блока, вычислив #O =π 10 — N/t = π214√10 — D вызовов оракула. Алгоритм Гровера может быть адаптирован для работы даже если количество решений заранее неизвестно, и даже если решений не существует. Хотя количество вызовов оракула определяет количество хэшей, которые должны быть сформированы, дополнительные накладные расходы будут связаны с вычислением каждого хэша, созданием соответствующего заголовка блока и квантовой коррекцией ошибок. Теперь проанализируем эти факторы, чтобы определить более реалистичную оценку времени работы двумя способами.  Во-первых, оцениваем время работы на основе хорошо изученной модели для универсальных квантовых компьютеров с коррекцией ошибок. На классическом компьютере хэш-функция, такая как SHA256, использует основные операции булевых ворот, в то время как на квантовом компьютере эти элементарные булевы ворота преобразуются в обратимые логические квантовые ворота, что влечет за собой некоторые накладные расходы. В протоколе SHA256 всего 64 раунда хэширования, и каждый раунд может быть выполнен с помощью оптимизированной схемы с 683 квантовыми вентилями (воротами) Тоффоли. Большинство квантовых кодов коррекции ошибок используют T-образные ворота, а не ворота Тоффоли в качестве представительных ворот, требующих больших затрат времени, и тщательный анализ затрат на выполнение вызова функции SHA256, а также инверсии относительно среднего, используемой в алгоритме Гровера, показывает, что общее количество T-образных ворот составляет 474168 для одного вызова оракула. При такой декомпозиции схемы T-гейты могут быть распараллелены только примерно в три раза. КК требуются дополнительные накладные расходы для выполнения коррекции ошибок. При выборе хорошего квантового кода коррекции ошибок необходимо учитывать множество компромиссов: толерантность к определенной физической модели ошибок, универсальность подпрограмм, количество используемых кубитов, сложность логических вентилей и объем классической обработки синдромов ошибок и обратной связи.  Приняв поверхностный код, который имеет преимущества относительно высокого порога ошибки отказоустойчивости и локальных измерений синдромов, можем адаптировать анализ… для оценки эффективности работы (для оценки общего времени работы квантового алгоритма). Время, необходимое для запуска алгоритма Гровера и успешной добычи блока, составляет: τ =#O×#G/s=π214√10-D×#G/s, где #G — количество циклов, необходимых для одного вызова оракула, а s — тактовая частота квантового компьютера. Используя поверхностный код, где доминирующие временные затраты приходятся на дистилляцию магических состояний для реализации T-образных ворот, можно найти #G = 297784 × cτ (D, pg), где первый коэффициент включает логическую глубину T-гейта для вызова функции SHA256 дважды, как того требует биткойн PoW, и ещё дважды, чтобы сделать схему обратимой, а также инверсию относительно среднего. Второй коэффициент, cτ , является коэффициентом накладных расходов времени, необходимых для квантовой коррекции ошибок. Он подсчитывает количество тактов на логические ворота T и является функцией сложности и коэффициента ошибок физических ворот pg. Для фиксированного коэффициента ошибок гейтов коэффициент накладных расходов cτ ограничен выше стоимостью инвертирования 256-битного хэша (максимальная сложность).  Поскольку квантовый алгоритм выполняет хэширование в суперпозиции, не существует прямого перевода квантовой вычислительной мощности в скорость хэширования. Однако мы можем определить эффективную скорость хеширования, hQC, как ожидаемое количество вызовов на классической машине, деленное на ожидаемое время поиска решения на квантовом компьютере, т.е. hQC ≡ N/t = 0.28×s√D. 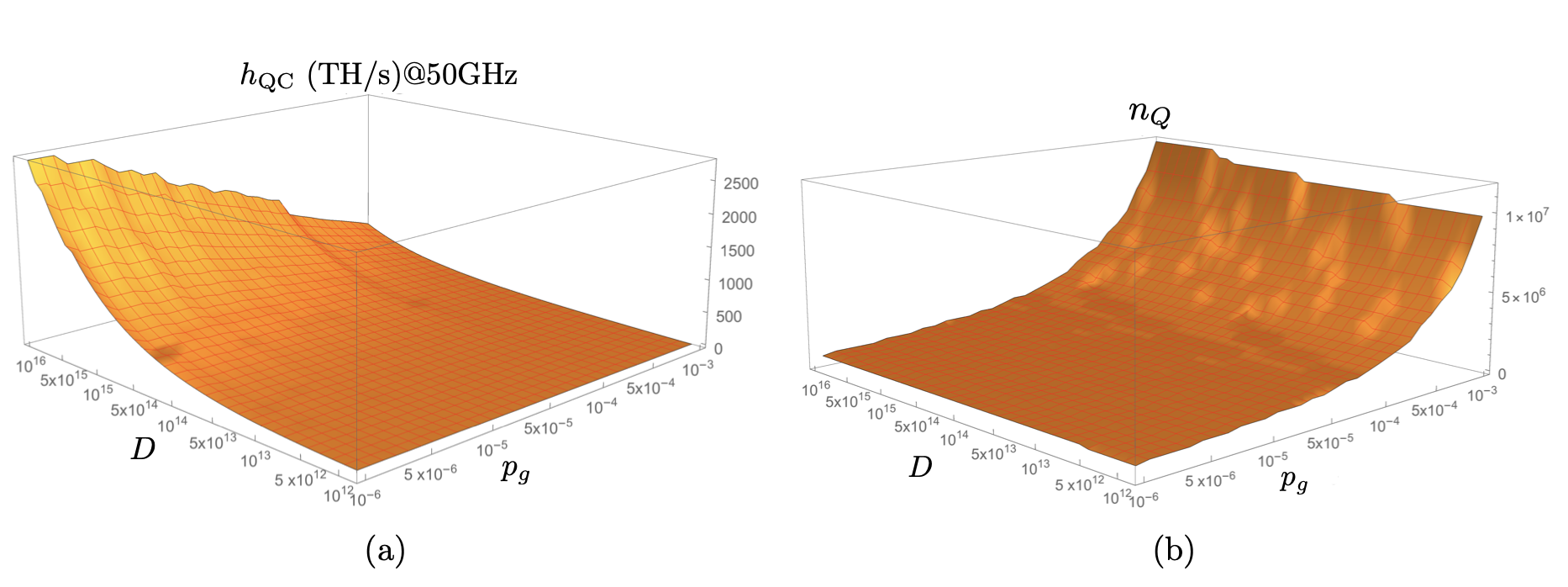РИС. 1. Производительность одного КК для атак на блокчейн в зависимости от коэффициента ошибок физических ворот pg, который является внутренней спецификацией машины, и сложности майнинга D, которая задается протоколом блокчейна. (a) Эффективный хэшрейт hQC для квантового компьютера, работающего на тактовой частоте 50 ГГц, которая находится на оптимистическом пределе прогнозируемых тактовых частот. Хэшрейт увеличивается как квадратный корень из сложности (обратите внимание на логарифмическую шкалу). Для d КК, работающих параллельно, эффективная скорость хеширования увеличивается в 2,56 раза × √d. (b) Количество физических кубитов nQ, используемых КК. Поскольку временные затраты ограничены, асимптотически эффективная скорость хэширования увеличивается как квадратный корень из сложности, что отражает квадратичное преимущество, получаемое от квантовых процессоров. Алгоритм Гровера может быть распараллелен на d квантовых процессоров. В оптимальной стратегии каждый процессор занимается поиском во всем пространстве потенциальных решений, и ожидаемое количество вызовов оракула, необходимое для нахождения решения, составляет #O = 0.39 × #O/√d. Отсюда следует, что ожидаемое время поиска решения составляет τ∥ = 0.39 × τ/√d, и эффективная скорость хэширования при параллельном использовании d квантовых процессоров составляет: hQC,∥ = 2.56 × hQC√d. Количество логических кубитов, необходимых в алгоритме Гровера, фиксировано и составляет 2402, независимо от сложности. Число необходимых физических кубитов равно nQ =2402×cnQ(D,pg), где cnQ — накладные расходы в пространстве, т.е. физические кубиты, возникающие из-за квантовой коррекции ошибок, и также является функцией сложности и частоты ошибок в гейтах. В приложении A показываем, как рассчитать временные и пространственные накладные расходы, связанные с исправлением ошибок. Результаты, показывающие производительность квантового компьютера для атак на блокчейн, приведены на рис. 1. Чтобы связать эти результаты с достижимыми характеристиками, мы сосредоточились на сверхпроводящих схемах, которые на данный момент имеют самую высокую скорость квантовых затворов среди квантовых технологий и предлагают перспективный путь к масштабируемости. Предполагая максимальную скорость затвора, достижимую на современных устройствах s = 66,7 МГц, и предполагая экспериментально сложную, но не невероятную, физическую скорость ошибки затвора pg = 5×10-4, и близкую к текущей сложности D = 1012, накладные расходы составляют cτ = 538,6 и cnQ = 1810,7, что подразумевает эффективную скорость хэширования hQC = 13,8 ГГц/с при использовании nQ = 4,4 × 106 физических кубитов. Это более чем в тысячу раз медленнее, нежели готовые ASIC-устройства, которые достигают скорости хэширования 14TH/s : причина же заключается в низкой скорости квантовых затворов и задержках для создания отказоустойчивых T-затворов. Квантовые технологии должны значительно расшириться в ближайшие десятилетия, и квантовая версия закона Мура, вероятно, будет действовать для квантовых тактовых частот, скорости затворов и количества кубитов. Ориентируясь на текущие улучшения в технологии сверхпроводящих квантовых схем, прогнозы таких улучшений приведены в Приложениях B и C. Это позволяет нам оценить мощность квантового компьютера как функцию времени, как показано на рисунке 2.  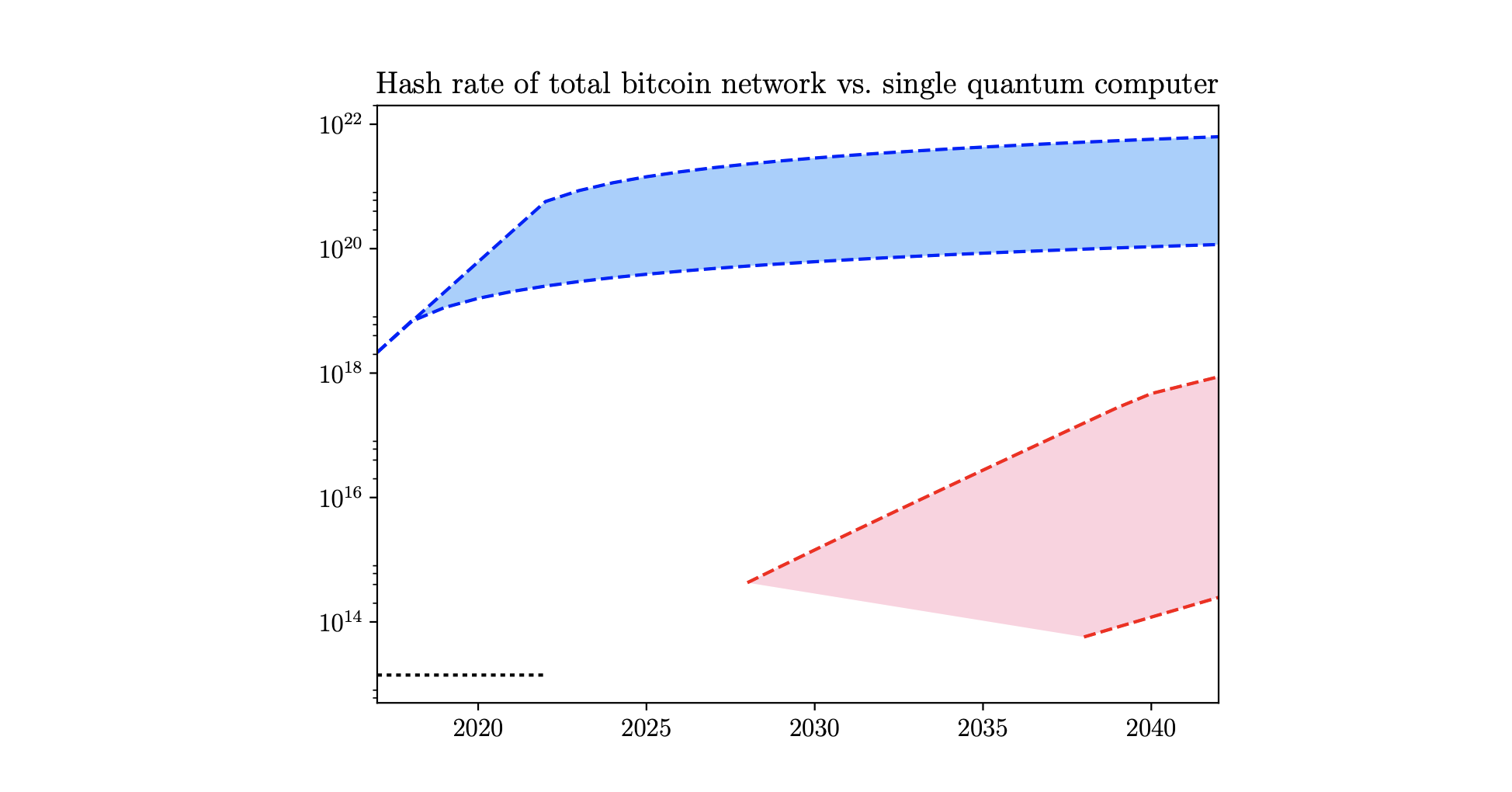РИС. 2. На этом графике показаны две оценки мощности хэширования (в хэшах в секунду) сети биткоина (синие полосатые кривые) по сравнению с одним КК (красные полосатые кривые) как функция времени в течение следующих 25 лет. Мы приводим более и менее оптимистичные оценки и области неопределённости (синяя и оранжевая области). Модель подробно описана в приложениях B и C. До 2028 года (по более оптимистичной оценке) не будет ни одного квантового компьютера с достаточным количеством кубитов для реализации алгоритма Гровера. Для сравнения, черная пунктирная линия показывает хэшрейт одного устройства ASIC сегодня. Очевидно, что пройдёт некоторое время, прежде чем КК превзойдут классические машины в решении этой задачи, а когда это произойдёт, один КК не будет иметь мощности, достаточной для хэширования. Однако даже при скромном улучшении мощности по сравнению с классическими машинами конкурирующих майнеров некоторые атаки становятся более прибыльными, например, атаки на майнинговые пулы, которые используют смарт-контракты для вознаграждения майнеров пула за сокрытия найденных блоков. Например, учитывая оптимистичные предположения, изложенные в Приложении A, где эффективная скорость хэширования имеет масштаб hQC = 0,04 × s√D, при D = 1013 и s = 50 ГГц, дробная мощность хэширования группы из 20 КК, работающих параллельно, относительно общей мощности хэширования составляет 0,1%. Это позволит осуществить квантовую атаку на пул майнинга с минимальными затратами на подкуп, что снизит доход пула на 10%. 

B. Атаки на подписи

Подписи в биткоине делаются с помощью алгоритма цифровой подписи на основе кривой secp256k1. Безопасность этой системы основана на трудности проблемы дискретного журнала эллиптической кривой (ECDLP). Хотя эта проблема всё ещё считается классически трудной, эффективный квантовый алгоритм для её решения был предложен Шором. Этот алгоритм означает, что достаточно большой универсальный КК может эффективно вычислить закрытый ключ, связанный с данным открытым ключом, что делает эту схему совершенно небезопасной.  Последствия для (Б/б)иткоина следующие:

1. (Повторное использование адресов) Чтобы потратить биткоин с адреса, необходимо раскрыть открытый ключ, связанный с этим адресом. Как только открытый ключ раскрывается в присутствии квантового компьютера, адрес больше не является безопасным и, следовательно, никогда не должен использоваться снова. Хотя использование свежих адресов уже является рекомендуемой практикой в Биткоине, на практике это не всегда соблюдается. Любой адрес, на котором есть биткойн и для которого был раскрыт открытый ключ, совершенно небезопасен.
2. (Обработанные транзакции) Если транзакция совершается с адреса, с которого ранее не проводились траты, и эта транзакция помещается в блокчейн с несколькими следующими за ней блоками, то такая транзакция достаточно надёжно защищена от квантовых атак. Закрытый ключ может быть получен из опубликованного открытого ключа, но так как адрес уже был потрачен, то для проведения атаки на двойную трату потребуется сочетание с пере-хешированием сети. Как увидим… даже с КК атака на двойную трату маловероятна, если транзакция имеет много блоков, следующих за ней.
3. (Необработанные транзакции) После того, как транзакция была передана в сеть, но до того, как она была помещена в блокчейн, она подвергается риску квантовой атаки. Если приватный ключ может быть получен из широковещательного открытого ключа до того, как транзакция будет помещена в блокчейн, то злоумышленник может использовать этот секретный ключ для широковещательной передачи новой транзакции с того же адреса на свой собственный адрес. Если злоумышленник затем убедится, что эта новая транзакция будет помещена в блокчейн первой, то он сможет эффективно украсть все биткоины, находящиеся за исходным адресом.

Мы рассматриваем пункт (3) как наиболее серьёзную атаку. Чтобы определить серьезность этой атаки, важно точно оценить, сколько времени потребуется квантовому компьютеру для вычисления ECDLP, и можно ли это сделать за время, близкое к интервалу между блоками. 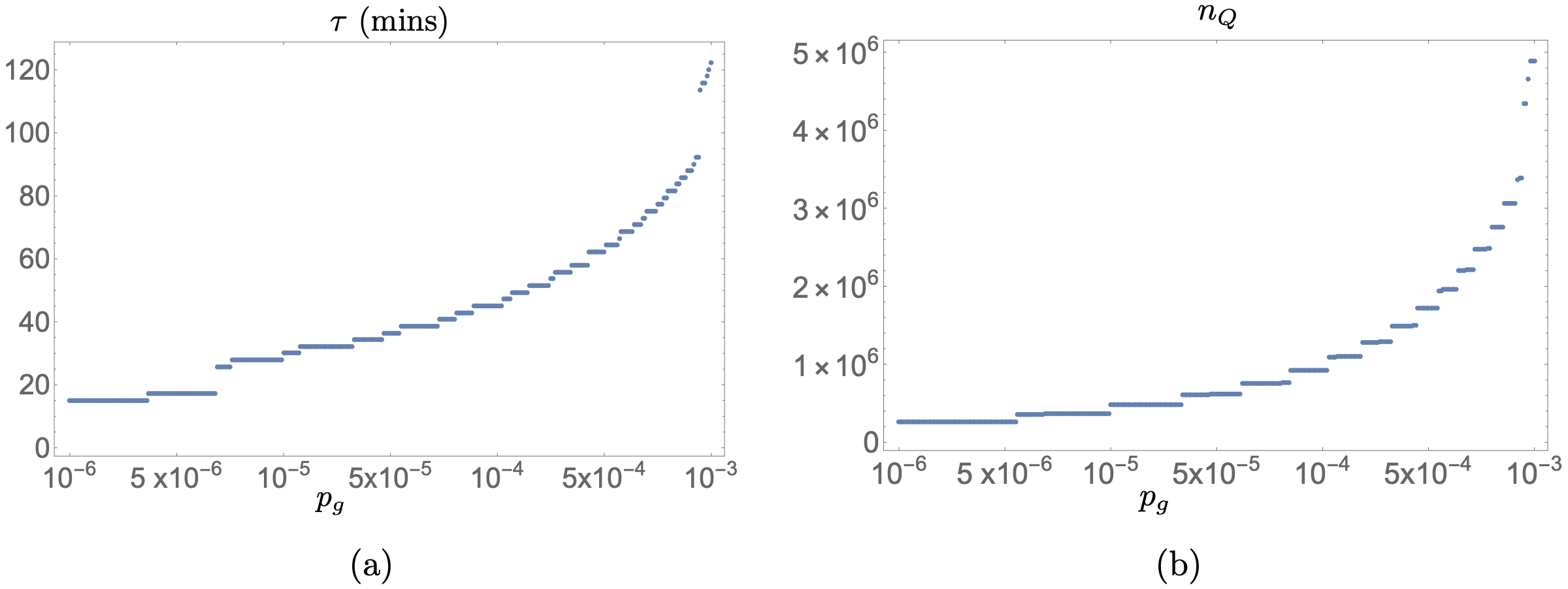РИС. 3. Производительность КК, работающего на тактовой частоте 10 ГГц, при атаках на цифровые подписи с использованием алгоритма цифровой подписи на эллиптической кривой. (a) Время в минутах для взлома подписи как функция коэффициента ошибок физических ворот pg. (b) Количество физических кубитов, используемых КК. Для случая с n-битовым простым полем недавно оптимизированный анализ показал, что КК может решить проблему, используя 9n + 2⌈log2(n)⌉ + 10 логических кубитов и (448 log2(n) + 4090)n3 вентиля (ворот) Тоффоли. Биткойн использует n = 256 битовых подписей, поэтому количество ворот Тоффоли составляет 1,28 × 1011, что может быть слегка распараллеленно до глубины 1,16 × 1011. Каждый ворот Тоффоли может быть реализован с помощью небольшой схемы с глубиной T затвора один, действующей на 7 кубитов параллельно (включая 4 вспомогательных кубита). Следуя анализу раздела III A, мы можем оценить ресурсы, необходимые для квантовой атаки на цифровые подписи. Как и при добыче блоков, основное время уходит на дистилляцию магических состояний для логических T-врат. Время решения ECDLP на квантовом процессоре составляет τ =1,28×1011 ×cτ(pg)/с, где временные затраты cτ теперь зависят только от частоты ошибок в затворах, а s — снова тактовая частота. Число необходимых физических кубитов равно: nQ =2334×cnQ(pg), где первый фактор — это количество логических кубитов, включая 4 логических кубита ancilla, а cnQ — это пространственные накладные расходы. Производительность КК для атаки на цифровые подписи приведена на рис. 3. При использовании поверхностного кода с коэффициентом ошибок физических ворот pg = 5 × 10-4, коэффициенты накладных расходов составляют cτ = 291,7 и cnQ = 735,3, а время решения задачи при тактовой частоте 66,6 МГц составляет 6,49 дня при использовании 1,7 × 106 физических кубитов. Если говорить о повышении производительности, то для тактовой частоты 10 ГГц и коэффициента ошибок 10-5 сигнатура взламывается за 30 минут с использованием 485550 кубитов. Последнее делает атаку в пункте (3) вполне возможной и сделает нынешнюю систему Биткоин крайне небезопасной. Оценка времени, необходимого КК для взлома схемы подписи, как функция времени, приведена на рисунке 4 на основе модели, описанной в приложениях B и C.  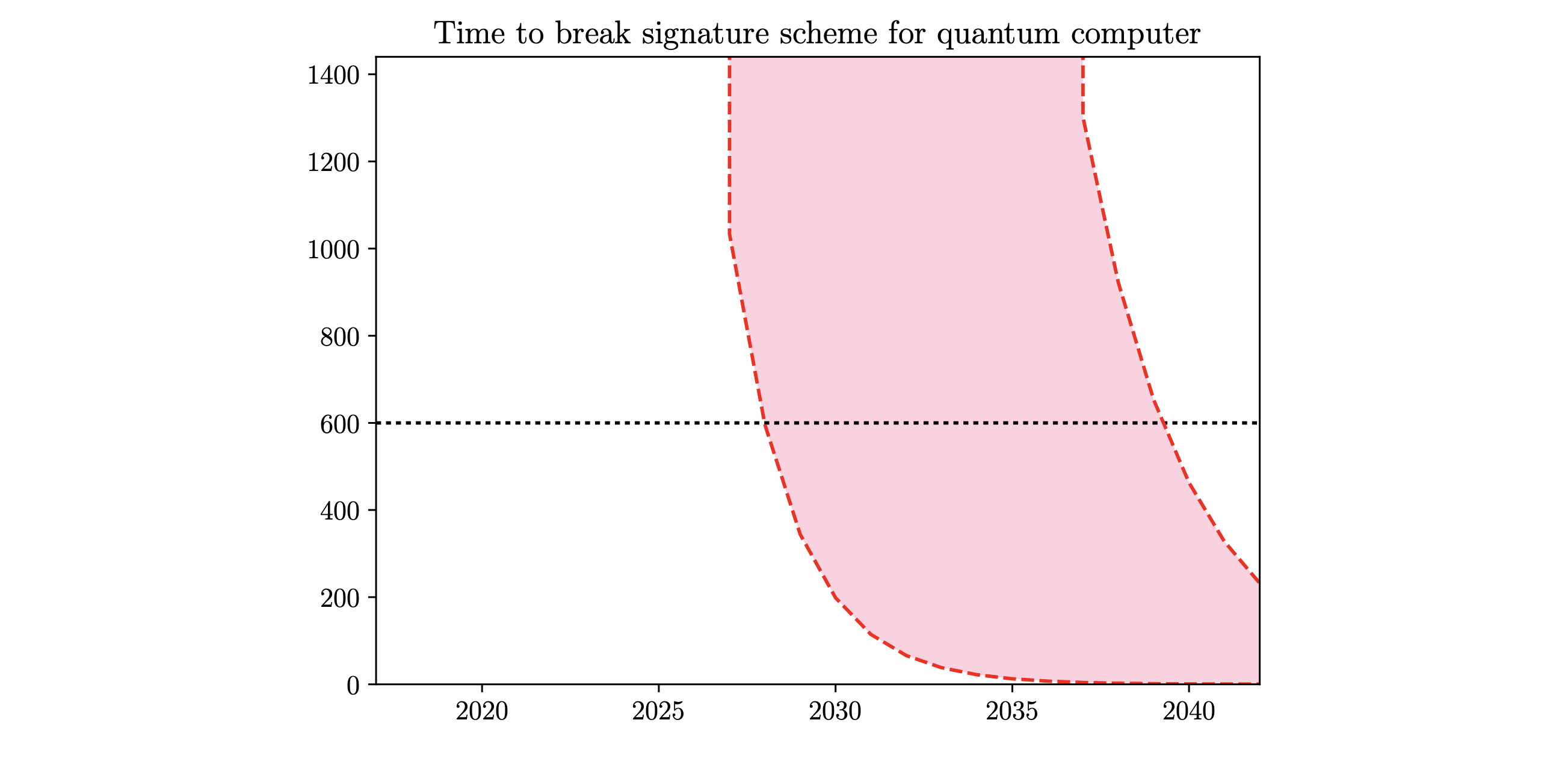РИС. 4. На этом графике показаны две оценки времени (в секундах), необходимого КК для взлома схемы подписи (красные кривые), как функция времени в течение следующих 25 лет. Мы приводим более и менее оптимистичные оценки (красные полосатые линии). Модели подробно описаны в Приложении С. Согласно этой оценке, схема подписи может быть взломана менее чем за 10 минут (600 секунд, черная пунктирная линия) уже в 2027 году.

C. Будущие усовершенствования квантовых атак

Мы описали атаки на протокол Bitcoin с использованием известных квантовых алгоритмов и схем коррекции ошибок. Хотя некоторые оценки скорости и масштабирования квантовых вычислений могут показаться (слишком) оптимистичными, важно помнить, что существует несколько путей повышения производительности квантовых компьютеров для решения вышеупомянутых проблем. Во-первых, предполагаемый код коррекции ошибок — поверхностный код, который требует значительных классических вычислительных затрат на дистилляцию состояний, выделение синдрома ошибки и коррекцию. Другие коды, которые позволяют использовать трансверсальные клиффордовские и неклиффордовские гейты, могли бы преодолеть необходимость медленной перегонки состояний. Фактически, замедление от классической обработки для извлечения и исправления синдромов может быть полностью устранено с помощью протокола без измерений… который в недавнем анализе показывает пороги ошибок только примерно в 5 раз хуже, чем поверхностный код с тяжелыми измерениями. Это потенциально может значительно повысить общую скорость исправления ошибок. Во-вторых, уменьшение количества логических вентилей квантовых схем возможно по мере разработки более эффективных передовых методов квантовых вычислений. Например, на примере конкретной задачи большого размера (включая оракульные реализации), которая была проанализирована в предыдущей работе, было проведено прямое сравнение количества конкретных вентилей, полученных с помощью программного пакета Quipper, между старым и новым квантовыми алгоритмами решения линейных систем, показавшее улучшение на несколько порядков . Учитывая, что квантовые алгоритмы Шора и Гровера были хорошо изучены и высоко оптимизированы, не стоит ожидать такого резкого улучшения, тем не менее, вероятно, что некоторое улучшение возможно. В-третьих, различные квантовые алгоритмы могут обеспечить относительное ускорение. В недавней работе (того же) Калиски представлен квантовый алгоритм для задачи дискретного логарифма: найти m при b = am, где b — известное целевое значение, а a — известное основание, используя запросы к так называемой подпрограмме «волшебного ящика», которая вычисляет старший бит m. Повторяя запросы с использованием разумно выбранных мощностей целевого значения, можно вычислить все биты m и решить задачу. Поскольку различные биты решаются по очереди, задача может быть распределена между несколькими квантовыми процессорами. Каждый процессор требует количество логических кубитов, сравнимое с решением всей задачи, но общее время будет сокращено за счет распараллеливания. Более того, накладные расходы на квантовую коррекцию ошибок, вероятно, уменьшатся, поскольку фазы в части схемы квантового преобразования Фурье не должны быть такими точными, как в оригинальном алгоритме Шора.

IV. ПРОТИВОПОКАЗАНИЯ 

A. Альтернативные доказательства работы

Как видели в предыдущем разделе, КК может использовать поиск Гровера для выполнения доказательства работы Биткоина, используя квадратично меньшее количество хэшей, чем требуется классически. В этом разделе мы исследуем альтернативные способы доказательства работы, которые могут дать меньшее квантовое преимущество. Основные свойства, которые мы хотим получить от доказательства работы, следующие:

1. (Сложность) Сложность задачи может быть скорректирована в соответствии с вычислительной мощностью, доступной в сети;
2. (Асимметрия) Гораздо проще проверить, что доказательство работы было успешно выполнено, чем выполнить его;
3. (Отсутствие квантового преимущества) Доказательство выполнения работы не может быть выполнено значительно быстрее с помощью КК, чем с помощью классического компьютера.

Доказательство работы биткоина удовлетворяет пунктам (1), (2), но мы хотели бы найти альтернативное доказательство работы, которое лучше справляется с (3). Аналогичные соображения были рассмотрены авторами, пытающимися найти доказательство работы, которое вместо (3) ищет доказательства работы, которые не могут быть ускорены ASIC. Один из подходов к этому — поиск доказательств работы, требующих много памяти. Для этого было предложено несколько интересных кандидатов, таких как Momentum, основанный на поиске коллизий в хэш-функции, Cuckoo Cycle, основанный на поиске подграфов постоянного размера в случайном графе, и Equihash, основанный на обобщенной проблеме дня рождения. Они также являются хорошими кандидатами на создание более квантово-устойчивого доказательства работы…

B. Обзор пост-квантовых схем подписи

В литературе было предложено множество предположительно квантово-безопасных схем подписи с открытым ключом. Примерами таких схем являются схемы подписи на основе хэшей… Каждая из этих криптосистем имеет разную степень эффективности. Сравнение по размеру подписи и размеру ключа приведено в таблице II. 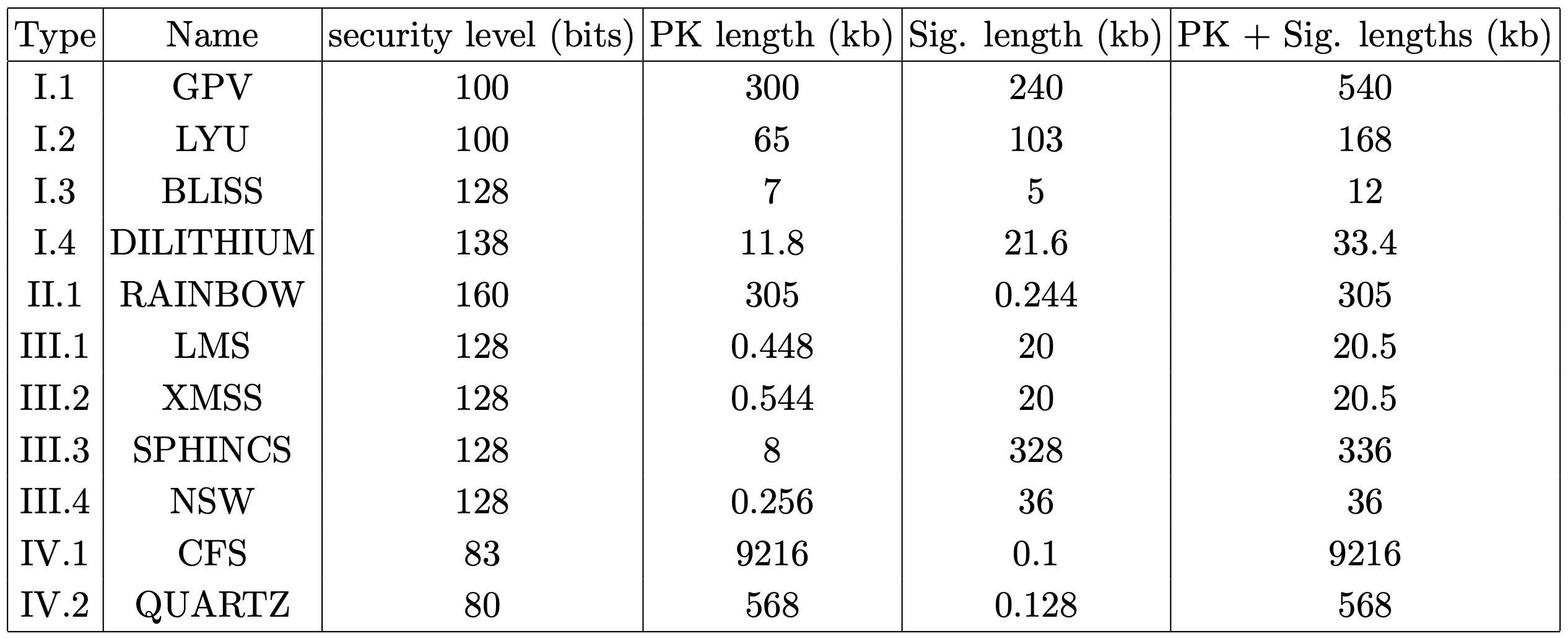ТАБЛИЦА II. Сравнение длины открытого ключа (PK) и подписи схем постквантовой подписи в килобитах (kb). Уровень безопасности указан для классических атак. Тип I основан на решетке, тип II — на многомерных полиномах, тип III — на хэшировании, тип IV — на коде.  В контексте блокчейна наиболее важными параметрами схемы подписи являются длина подписи и открытого ключа, поскольку они должны храниться в некотором объеме для полной проверки транзакций, а также время проверки подписи. Если взглянуть на таблицу II, то в отношении суммы длин подписи и открытого ключа единственными разумными вариантами являются схемы на основе хэша и решетки. Схемы на основе хэша, такие как XMSS, имеют то преимущество, что их безопасность доказуема, по крайней мере, при условии, что выбранная хэш-функция ведет себя как случайный оракул. Общая квантовая атака против этих схем заключается в использовании алгоритма Гровера, что означает, что их квантовый уровень безопасности составляет половину классического уровня безопасности. В отличие от этого, наиболее известная квантовая атака против DILITHIUM при классическом уровне безопасности в 138 бит требует времени 2125. Таким образом, при одинаковом уровне квантовой безопасности схемы на основе решётки имеют некоторое преимущество в длине подписи и открытого ключа. ТАБЛИЦА III. Алгоритмы для вычисления пространственных и временных ресурсов для квантовых атак. Входы: pg — коэффициент ошибок физических ворот; nC — общее количество ворот Клиффорда в логической схеме; nT — общее количество ворот T в логической схеме; и nL — количество логических кубитов. Выходными данными являются τ — временные затраты в количестве тактовых циклов; и nQ = Qcircuit + Qfactory — количество физических кубитов, используемых для вычислений, включая дистилляцию состояний.

Заключение

Таким образом, эта статья стала отправной точкой исследований влияния КК на защищённость ДРС, блокчейна — в частности, но на сегодня технологии и там, и там шагнули далеко вперёд, а потому нас ждут новые исследования, но на сегодня — всё  и потому —  До!