Перевод
Это вольный перевод статьи В. Бутерина: vitalik.ca/general/2023/01/20/stealth.html.
Введение
Одна из самых больших проблем в экосистеме Ethereum — конфиденциальность. По умолчанию всё, что попадает в публичный блокчейн, является публичным. Всё чаще это означает не только деньги и финансовые транзакции, но и имена ENS, POAP, NFT, токены soulbound и многое другое. На практике использование всего набора приложений Ethereum подразумевает обнародование значительной части вашей жизни для всеобщего обозрения и анализа.
Улучшение такого положения дел является важной проблемой, и это широко признаётся (сообществом). Однако до сих пор дискуссии об улучшении приватности в основном велись вокруг одного конкретного случая использования: сохранение приватности переводов ETH и основных токенов ERC20. В этом посте опишем механику и примеры использования другой категории инструментов, которые могут улучшить состояние приватности в Ethereum в ряде других контекстов: скрытые адреса (буквально — стелс-адреса).
Что такое скрытая адресная система?
Предположим, что Алиса хочет отправить Бобу актив. Это может быть некоторое количество криптовалюты (например, 1 ETH, 500 DAI), или это может быть NFT. Когда Боб получает актив, он не хочет, чтобы весь мир знал, что именно он его получил. Скрыть факт передачи невозможно, особенно если это NFT, у которого есть только одна ончейн-копия, но скрыть, кто является получателем, может быть гораздо более жизнеспособным. Алиса и Боб ленивы (и экономны): они хотят систему, в которой процесс оплаты точно такой же, как и сегодня. Боб посылает Алисе (или регистрируется в ENS) некий «адрес», кодирующий, как кто-то может ему заплатить, и одной этой информации достаточно, чтобы Алиса (или любой другой человек) отправила ему актив.
Обратите внимание, что это другой вид конфиденциальности, нежели тот, который обеспечивает, например, Tornado Cash. Tornado Cash может скрыть переводы основных взаимозаменяемых активов, таких как ETH или основные ERC-20 (хотя он наиболее удобен для приватной отправки самому себе), но он очень слаб в добавлении конфиденциальности к переводам иных ERC20, и он вообще не может добавить конфиденциальности к переводам NFT.
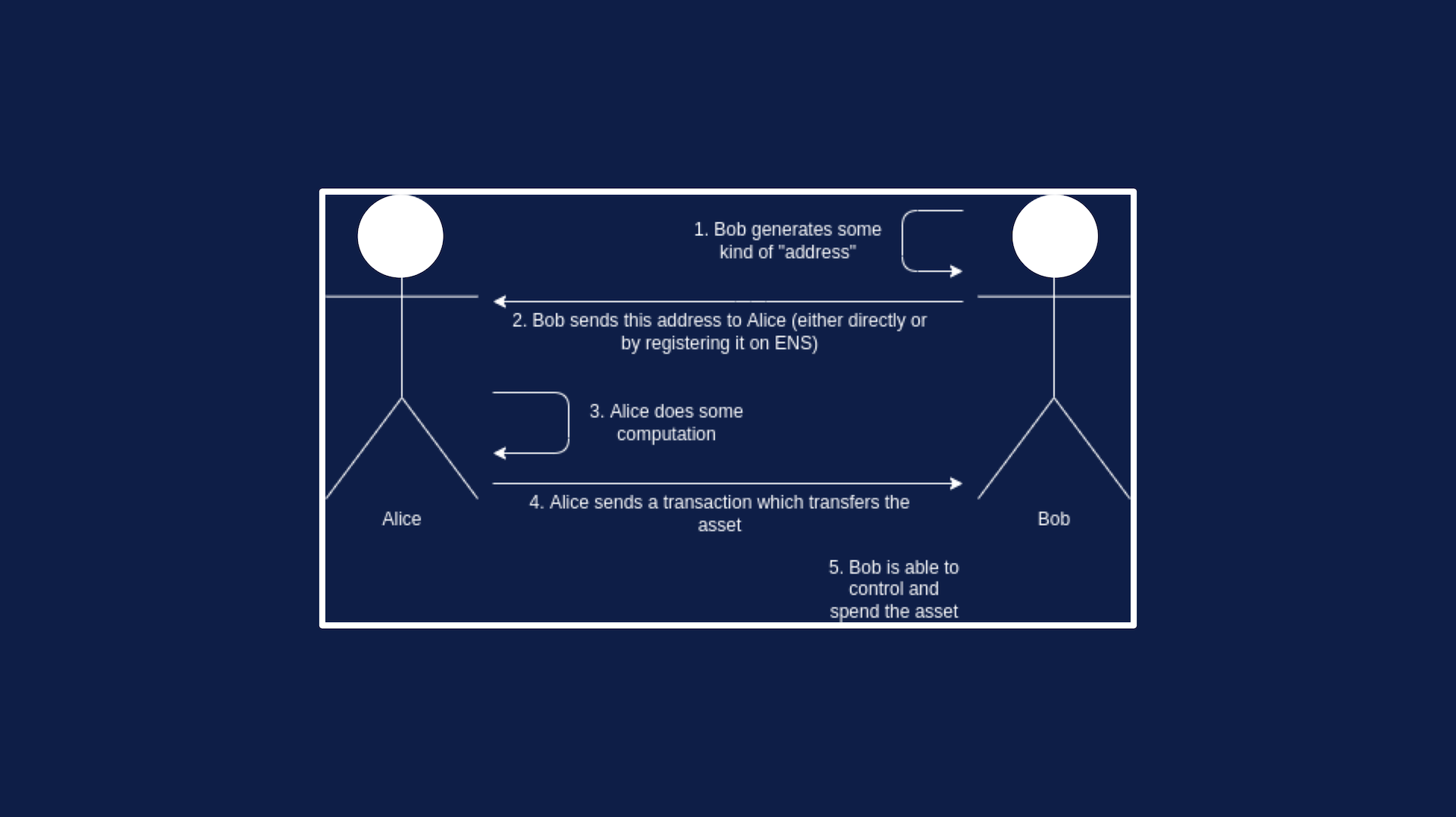Обычный рабочий процесс совершения платежа с помощью криптовалюты. Мы хотим добавить конфиденциальность (никто не сможет сказать, что именно Боб получил актив), но сохранить рабочий процесс прежним.
Скрытые адреса обеспечивают такую схему. Скрытый адрес — адрес, который может быть сгенерирован как Алисой, так и Бобом, но контролировать который может только Боб. Боб генерирует и хранит в секрете ключ для расходования средств и использует этот ключ для генерации скрытого мета-адреса. Он передаёт этот мета-адрес Алисе (или регистрирует его в ENS). Алиса может произвести вычисления на этом мета-адресе, чтобы сгенерировать скрытый адрес, принадлежащий Бобу. Затем она может отправить любые активы, которые она хочет отправить на этот адрес, и Боб будет иметь полный контроль над ними. Вместе с передачей она публикует ончейн некоторые дополнительные криптографические данные (эфемерный pubkey), которые помогают Бобу обнаружить, что этот адрес принадлежит ему.
Другой способ посмотреть на это: стелс-адреса обеспечивают те же свойства конфиденциальности, что и генерирование Бобом свежего адреса для каждой транзакции, но не требуют никакого взаимодействия со стороны Боба.
Полный рабочий процесс схемы скрытых адресов можно представить следующим образом:
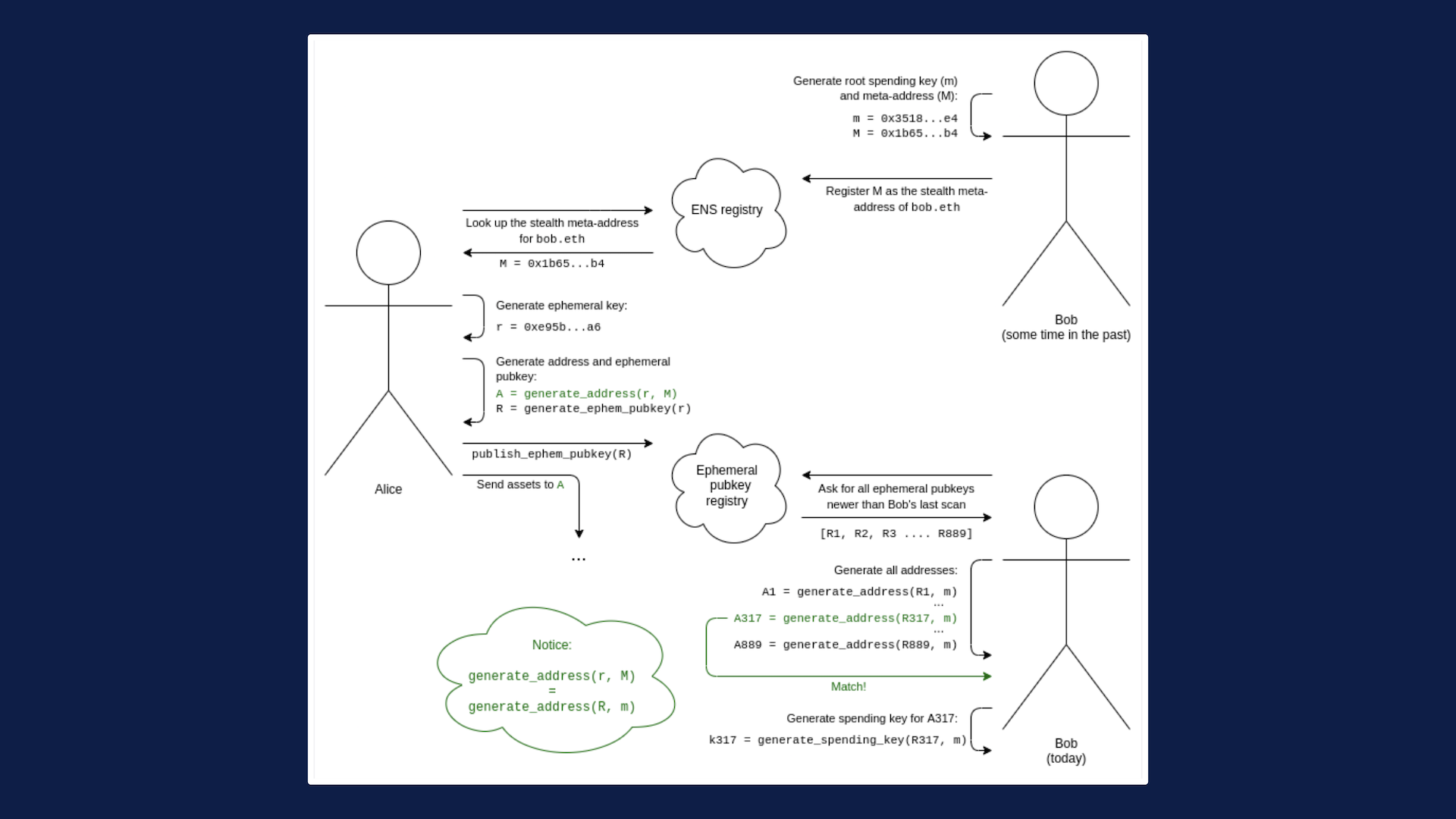(Вот что происходит именно):
- Боб генерирует свой корневой ключ трат (m) и скрытый мета-адрес (M).
- Боб добавляет запись ENS для регистрации M в качестве скрытого мета-адреса для bob.eth.
- Мы предполагаем, что Алиса знает, что Боб — bob.eth. Алиса ищет его скрытый мета-адрес M в ENS.
- Алиса генерирует эфемерный ключ, который известен только ей и который она использует только один раз (для генерации этого конкретного скрытого адреса).
- Алиса использует алгоритм, который объединяет её эфемерный ключ и мета-адрес Боба для создания скрытого адреса. Теперь она может отправлять активы на этот адрес.
- Алиса также генерирует свой эфемерный открытый ключ и публикует его в реестре эфемерных открытых ключей (это может быть сделано в той же транзакции, что и первая транзакция по отправке активов на этот стелс-адрес).
- Чтобы Боб обнаружил принадлежащие ему скрытые адреса, Бобу необходимо просканировать реестр эфемерных открытых ключей на предмет всего списка эфемерных открытых ключей, опубликованных кем-либо по любой причине с момента последнего сканирования.
- Для каждого эфемерного открытого ключа Боб пытается объединить его со своим корневым ключом трат для создания скрытого адреса и проверяет, есть ли в этом адресе какие-либо активы. Если есть, Боб вычисляет ключ трат для этого адреса и запоминает его.
Всё это основано на двух видах криптографической хитрости. Во-первых, нам нужна пара алгоритмов для создания общего секрета: один алгоритм, который использует секрет Алисы (её эфемерный ключ) и открытый ключ Боба (его мета-адрес), и другой алгоритм, который использует секрет Боба (его корневой расходный ключ) и открытый ключ Алисы (её эфемерный открытый ключ). Это можно сделать многими способами; обмен ключами Диффи-Хеллмана был одним из результатов, которые основали область современной криптографии, и он достигает именно этого.
Но общего секрета самого по себе недостаточно: если просто сгенерируем закрытый ключ из общего секрета, то и Алиса, и Боб смогут тратить с этого адреса (средства). Мы могли бы оставить всё как есть, предоставив Бобу самому переводить средства на новый адрес, но это неэффективно и без необходимости снижает безопасность. Поэтому мы также добавляем механизм “ослепления” ключей (слепая подпись — см. ниже): пару алгоритмов, в которых Боб может объединить общий секрет со своим корневым ключом трат, а Алиса может объединить общий секрет с мета-адресом Боба таким образом, что Алиса может сгенерировать скрытый адрес, а Боб может сгенерировать ключ трат для этого скрытого адреса, и всё это без создания открытой связи между скрытым адресом и мета-адресом Боба (или между одним скрытым адресом и другим).
Скрытые адреса с использованием криптографии эллиптической кривой
Скрытые адреса с использованием криптографии эллиптических кривых были первоначально представлены в контексте Биткоина Питером Тоддом в 2014 году.
Эта техника работает следующим образом (это предполагает предварительное знание основ криптографии на эллиптических кривых):
- Боб генерирует ключ m и вычисляет M = G * m, где G — общепринятая точка генератора для эллиптической кривой. Скрытый мета-адрес является кодировкой M.
- Алиса генерирует эфемерный ключ r и публикует эфемерный открытый ключ R = G * r.
- Алиса может вычислить общий секрет S = M * r, а Боб может вычислить такой же общий секрет S = m * R.
В общем, и в Bitcoin, и в Ethereum (включая ERC-4337) адрес — это хэш, содержащий открытый ключ, используемый для проверки транзакций с этого адреса. Таким образом, можете вычислить адрес, если вычислите открытый ключ. Чтобы вычислить открытый ключ, Алиса или Боб могут вычислить P = M + G * hash(S).
Чтобы вычислить закрытый ключ для этого адреса, Боб (и только Боб) может вычислить p = m + hash(S).
Это удовлетворяет всем нашим требованиям, изложенным выше, и является удивительно простым!
Сегодня даже существует EIP, пытающийся определить стандарт скрытых адресов для Ethereum, который одновременно поддерживает этот подход и даёт возможность пользователям разрабатывать другие подходы (например, поддерживающие наличие у Боба отдельных ключей траты и просмотра, или использующие другую криптографию для квантово-устойчивой безопасности).
Теперь можете подумать (вот над чем): скрытые адреса не так уж сложны, теория уже проработана, и их внедрение — лишь деталь реализации. Проблема, однако, в том, что есть несколько довольно крупных деталей реализации, через которые должна пройти действительно эффективная реализация.
Скрытые адреса и оплата комиссионных за транзакции
Предположим, что кто-то посылает вам NFT. Памятуя о вашей конфиденциальности, они отправляют его на скрытый адрес, который вы контролируете.
После сканирования эфемерных ключей ваш кошелек автоматически обнаруживает этот адрес. Теперь вы можете свободно подтвердить право собственности на NFT или передать его кому-то другому.
Но есть проблема! На этом счёте 0 ETH, и поэтому нет возможности оплатить комиссию за транзакцию. Даже платёжные системы для токенов ERC-4337 не работают, потому что они работают только для взаимозаменяемых токенов ERC20. И не можете отправить ETH на него со своего основного кошелька, потому что тогда создадите публично видимую ссылку.
Есть один «лёгкий» способ решить проблему: просто использовать ZK-SNARKs для перевода средств, чтобы оплатить сборы! Но это стоит много газа, дополнительные сотни тысяч газа только для одного перевода.
Другой умный подход предполагает доверие к специализированным агрегаторам транзакций («искателям«/searchers на жаргоне MEV).
Эти агрегаторы позволят пользователям заплатить один раз, чтобы приобрести набор «билетов», которые можно использовать для оплаты транзакций. Когда пользователю нужно потратить NFT на скрытый адрес, не содержащий ничего другого, он предоставляет агрегатору один из билетов, закодированный с помощью схемы слепой подписи Чаума (альтернативно).
Это оригинальный протокол, который использовался в централизованных схемах электронной наличности с сохранением конфиденциальности, предложенных в 1980-х и 1990-х годах.
Искатель принимает “билет” и неоднократно бесплатно включает транзакцию в свою связку, пока транзакция не будет успешно принята в блокчейне. Поскольку количество задействованных средств невелико, и они могут быть использованы только для оплаты транзакций, вопросы доверия и регулирования гораздо ниже, чем при «полной» реализации такого рода централизованной электронной наличности с сохранением конфиденциальности.
Скрытые адреса и разделение ключей расходов и просмотра
Предположим, что вместо того, чтобы у Боба был один главный «корневой ключ трат», который может делать всё, Боб хочет иметь отдельный корневой ключ трат и ключ просмотра.
Ключ просмотра может видеть все скрытые адреса Боба, но не может тратить с них деньги.
В мире эллиптических кривых это можно решить с помощью очень простого криптографического трюка:
- Мета-адрес Боба M теперь имеет форму (K, V), кодирующую G * k и G * v, где k — ключ траты, а v — ключ просмотра.
- Общий секрет теперь S = V * r = v * R, где r по-прежнему является эфемерным ключом Алисы, а R по-прежнему является эфемерным открытым ключом, который Алиса публикует.
- Открытый ключ скрытого адреса — P = K + G * hash(S), а закрытый ключ — p = k + hash(S).
Обратите внимание, что первый умный криптографический шаг (генерация общего секрета) использует ключ просмотра, а второй умный криптографический шаг (параллельные алгоритмы Алисы и Боба для генерации скрытого адреса и его закрытого ключа) использует корневой ключ расходов.
Это имеет множество вариантов использования. Например, если Боб хочет получать POAP, то Боб может дать своему POAP-кошельку (или даже не очень безопасному веб-интерфейсу) ключ просмотра для сканирования и просмотра всех своих POAP, не давая этому интерфейсу полномочий тратить эти POAP.
Скрытые адреса и более простое сканирование
Чтобы облегчить сканирование всего набора эфемерных открытых ключей, один из методов — добавить тег представления к каждому эфемерному открытому ключу.
Один из способов сделать это в приведённом выше механизме — сделать так, чтобы меткой просмотра был один байт общего секрета (например, x-координата S по модулю 256 или первый байт hash(S)).
Таким образом, Бобу нужно выполнить только одно умножение эллиптической кривой для каждого эфемерного открытого ключа, чтобы вычислить общий секрет, и только в 1/256 случаев Бобу придется выполнять более сложные вычисления для генерации и проверки полного адреса.
Скрытые адреса и квантово-устойчивая безопасность
Приведённая выше схема зависит от эллиптических кривых, которые великолепны, но, к сожалению, уязвимы для квантовых компьютеров. Если квантовые компьютеры станут проблемой, нам придётся перейти на квантово-устойчивые алгоритмы.
Для этого есть два естественных кандидата: изогении эллиптических кривых и решётки (см. также по ссылке).
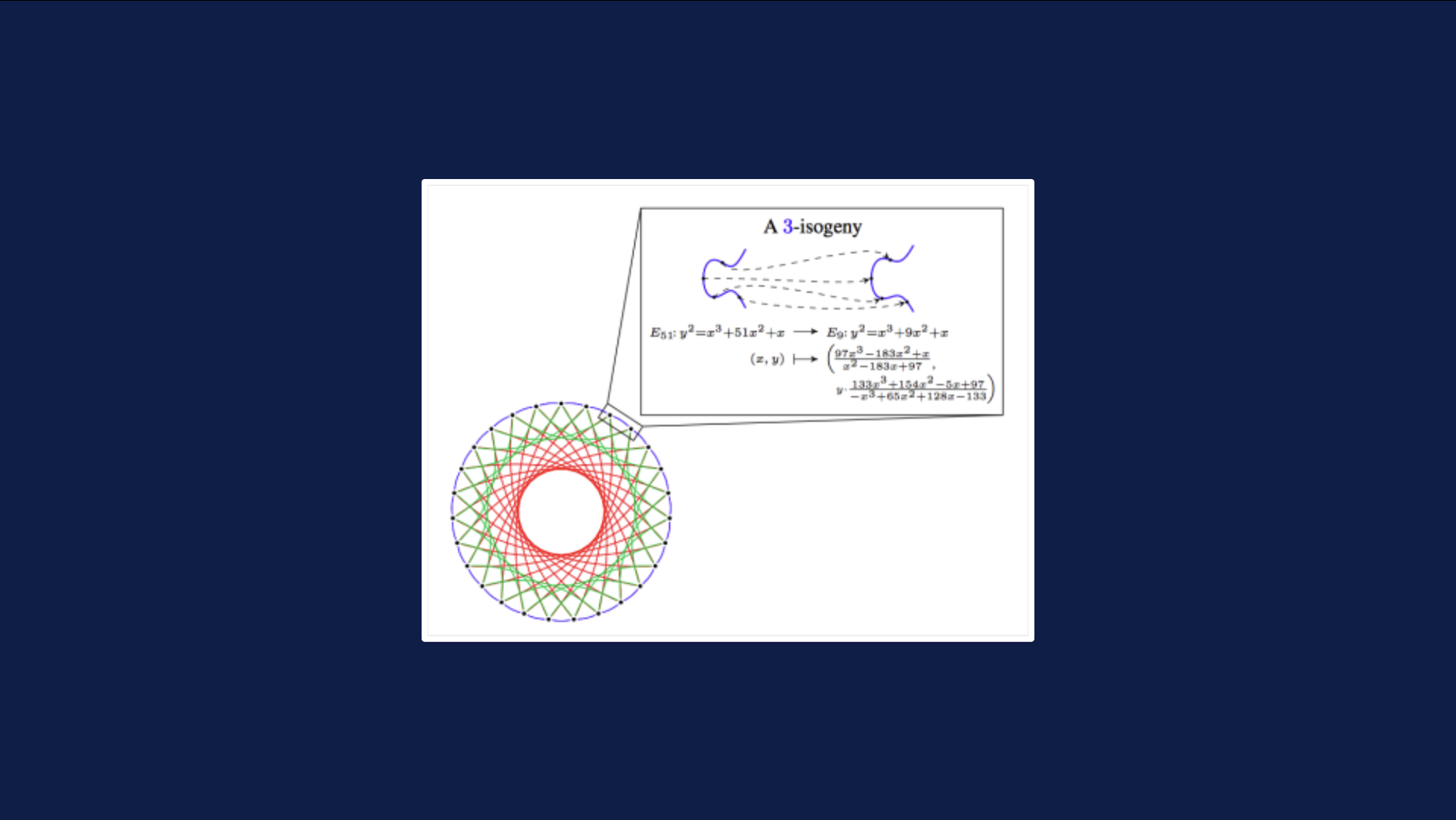
Изогении эллиптических кривых — совершенно другая математическая конструкция, основанная на эллиптических кривых, которая обладает свойствами линейности, позволяющими нам делать криптографические трюки, аналогичные тем, что делали выше, но при этом ловко избегает построения циклических групп, которые могут быть уязвимы для атак на дискретный логарифм с помощью квантовых компьютеров.
Основным недостатком криптографии на основе изогении является очень сложная математика, лежащая в её основе, и риск того, что возможные атаки скрыты под этой сложностью. Некоторые протоколы на основе изогений были взломаны в прошлом году, хотя другие остаются безопасными. Главной сильной стороной изогений является относительно небольшой размер ключа и возможность прямого переноса многих видов подходов на основе эллиптических кривых.
Решётки — совершенно другая криптографическая конструкция, которая опирается на гораздо более простую математику, чем изогении эллиптических кривых, и способна на некоторые очень мощные вещи (например, полностью гомоморфное шифрование). На решётках могут быть построены схемы скрытых адресов, хотя разработка лучшей из них является открытой проблемой. Однако конструкции на основе решёток, как правило, имеют гораздо большие размеры ключей.
Полностью гомоморфное шифрование, применение решеток. Также может быть использовано для помощи протоколам скрытых адресов другим способом: чтобы помочь Бобу передать вычисления по проверке всей цепочки на наличие скрытых адресов, содержащих активы, не раскрывая свой ключ просмотра.
Третий подход заключается в построении схемы скрытого адреса из общих примитивов «чёрного ящика»: базовых компонентов, которые нужны многим людям по другим причинам.
Часть схемы, связанная с генерацией общего секрета, напрямую связана с обменом ключами — важным компонентом в системах шифрования с открытым ключом. Самая сложная часть — параллельные алгоритмы, которые позволяют Алисе генерировать только скрытый адрес (но не ключ расходов) и позволяют Бобу генерировать ключ расходов.
К сожалению, невозможно построить стелс-адреса из ингредиентов, более простых, чем те, которые требуются для создания системы шифрования с открытым ключом.
Существует простое доказательство этого: можете построить систему шифрования с открытым ключом из схемы скрытых адресов. Если Алиса хочет зашифровать сообщение Бобу, она может послать N транзакций, каждая из которых направляется либо на скрытый адрес, принадлежащий Бобу, либо на скрытый адрес, принадлежащий ей самой, а Боб может посмотреть, какие транзакции он получил, чтобы прочитать сообщение.
Это важно, потому что существуют математические доказательства того, что не можете выполнить шифрование с открытым ключом, используя только хэши, в то время как можете выполнить доказательство нулевого разглашения информации, используя только хэши — следовательно, скрытые адреса не могут быть выполнены с использованием только хэшей.
Вот один подход, который использует относительно простые компоненты: ZKP, которые могут быть сделаны из хэшей, и (скрывающее ключ) шифрования с открытым ключом.
Мета-адрес Боба — открытый ключ шифрования плюс хэш h = hash(x), а его расходный ключ — соответствующий ключ расшифровки плюс x.
Чтобы создать скрытый адрес, Алиса генерирует значение c и публикует в качестве своего эфемерного открытого ключа шифрование c, доступное для чтения Бобу. Сам адрес представляет собой счет ERC-4337, код которого проверяет транзакции, требуя, чтобы они сопровождались доказательством нулевого знания, подтверждающим владение значениями x и c, такими, что k = hash(hash(x), c) (где k является частью кода счета). Зная x и c, Боб может самостоятельно восстановить адрес и его код.
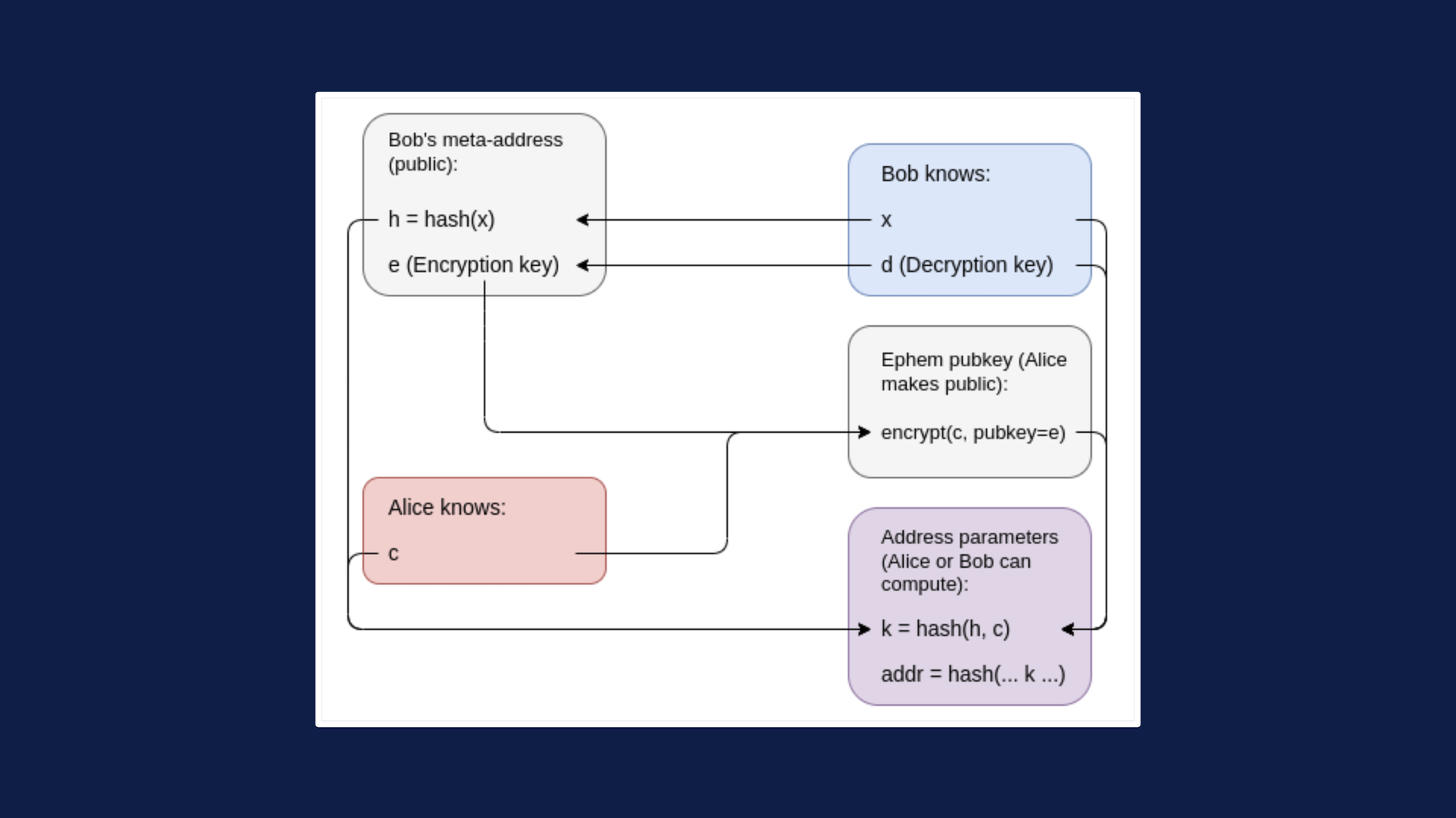Шифрование c никому, кроме Боба, ничего не говорит, а k — это хэш, поэтому он почти ничего не раскрывает о c. Сам код кошелька содержит только k, а закрытость c означает, что k нельзя отследить до h.
Однако для этого требуется STARKs, а STARKs очень большие. В конечном счёте, думаю, что в мире Ethereum после квантования будет много приложений, использующих множество STARKs, и поэтому я бы выступал за протокол агрегации, подобный описанному здесь, чтобы объединить все эти STARKs в один рекурсивный STARK для экономии места.
Stealth-адреса и социальное восстановление, а также кошельки multi-L2
В течение долгого времени я был поклонником кошельков социального восстановления: кошельки, которые имеют механизм мультисига с ключами, разделёнными между некоторой комбинацией учреждений, ваших других устройств и ваших друзей, где некоторое супер-большинство этих ключей может восстановить доступ к вашей учетной записи, если вы потеряете свой основной ключ.
Однако кошельки с социальным восстановлением не очень хорошо сочетаются со стелс-адресами: если нужно восстановить свой счёт (то есть, изменить, какой закрытый ключ его контролирует), также придётся выполнить определённый шаг, чтобы изменить логику проверки счёта на N стелс-кошельках, а это потребует N транзакций, что приведёт к высокой стоимости комиссии, (не) удобству и конфиденциальности.
Аналогичная проблема существует при взаимодействии социального восстановления и мира с несколькими протоколами второго уровня: если у вас есть аккаунт на Optimism, и на Arbitrum, и на Starknet, и на Scroll, и на Polygon, и, возможно, некоторые из этих рулонов имеют дюжину параллельных экземпляров по причинам масштабирования, и у вас есть аккаунт на каждом из них, то смена ключей может быть действительно сложной операцией.
Изменение ключей для многих учётных записей во многих цепочках требует огромных усилий.
Один из подходов заключается в том, чтобы смириться с тем, что восстановление происходит редко, и вполне допустимо, что оно будет дорогостоящим и болезненным.
Возможно, для снижения эффективности привязки по времени можете использовать автоматизированное программное обеспечение, которое будет переводить активы на новые скрытые адреса через случайные промежутки времени в течение двух недель. Но это далеко не идеальный вариант.
Другой подход заключается в секретном обмене корневым ключом между хранителями вместо использования восстановления смарт-контракта. Однако это лишает опекуна возможности деактивировать свои полномочия, чтобы помочь восстановить аккаунт, и поэтому в долгосрочной перспективе является рискованным.
Более сложный подход предполагает использование ZKP.
Рассмотрим схему на основе ZKP, описанную выше, но изменим логику следующим образом. Вместо того чтобы счёт напрямую хранил k = hash(hash(x), c), он будет хранить (скрывая) обязательство о местоположении k ончейн. Трата средств с этого счёта потребует предоставления доказательства с нулевым уровнем знаний, что (i) знаете место ончейн, соответствующее этому обязательству, и (ii) объект в этом месте содержит некоторое значение k (которое не раскрываете), и что у вас есть некоторые значения x и c, которые удовлетворяют k = hash(hash(x), c).
Это позволяет многим учётным записям, даже во многих протоколах второго уровня, контролироваться одним значением k где-то (на базовой цепочке или на каком-то втором уровне), где изменение этого одного значения достаточно, чтобы изменить права собственности всех ваших учетных записей, и все это без раскрытия связи между вашими учетными записями и друг другом.
Выводы
Базовые стелс-адреса могут быть реализованы довольно быстро уже сегодня и могут стать значительным стимулом для практической конфиденциальности пользователей в Ethereum.
Правда, для их поддержки требуется определённая работа со стороны кошелька.
Тем не менее, считаю, что кошельки должны начать двигаться к более естественной многоадресной модели (например, создание нового адреса для каждого приложения, с которым вы взаимодействуете, может быть одним из вариантов) и по другим причинам, связанным с конфиденциальностью.
Однако стелс-адреса создают некоторые долгосрочные проблемы, связанные с удобством использования, такие как сложность социального восстановления.
Возможно, пока можно просто принять эти проблемы, например, смириться с тем, что социальное восстановление будет связано либо с потерей конфиденциальности, либо с двухнедельной задержкой для медленного выпуска транзакций по восстановлению различных активов (что может быть обработано сторонней службой).
В долгосрочной перспективе эти проблемы могут быть решены, но экосистема стелс-адресов в долгосрочной перспективе выглядит как экосистема, которая будет очень сильно зависеть от ZKP.
Заключение
Рекомендую изучить все предыдущие статьи цикла, чтобы оценить ZKP перспективы полностью:
- https://hub.forklog.com/dokazatelstvo-nulevogo-razglasheniya-informatsii-vvodnoe-rukovodstvo/
- https://hub.forklog.com/zk-starks-vs-zk-snarks-razlichiya-v-tehnologiyah/
- https://hub.forklog.com/obzor-arhitektury-scroll/
На этом всё и —
До!